我同意其他答案，即這可能是直方圖的偽像。我可以謙虛地提供一些其他方法來繪製這些成績嗎？ >並可能是基本離散的基礎數據生成過程。

R代碼：

  require（hdrcde）require（Hmisc）require（denstrip）require（beanplot）require（beeswarm） ）等級<- c（1.2、1.4、1.4、1.9、2.0、2.3、2.6、2.6、3.4、4.2、4.2、4.3、4.6、4.6、4.8、4.8、4.9、5.3、6.0、6.2、6.4、7.1， 7.8，7.8）opar <- par（mfrow = c（1,6），mar = c（3,2,4,1））boxplot（grades，col =“ gray90”，main =“ Standard \ nboxplot”，yaxt =“ n”）hdr.boxplot（grade，main =“ HDR \ nboxplot”，yaxt =“ n”）bpplot（grades，xlab =“”，name = FALSE，main =“ Box-Percentile \ nPlot”）beanplot（等級，col =“灰色”，yaxt =“ n”，main =“ Bean情節/ \ nViolin情節”，border =“ black”）情節（c（0,2），range（grades），type =“ n” ，xaxt =“ n”，yaxt =“ n”，xlab =“”，ylab =“”，main =“ Density \ nplot”）denstrip（等級，horiz = FALSE，at = 1，寬度= 1）beeswarm（等級，pch = 19，main =“ Beesw arm \ nplot“）par（opar） 

編輯：（對不起，我是統計學家，我幫不上忙...）我去拿了 Jack的內核密度估計並從中重新採樣了24位“學生”。在每種情況下，我都繪製了直方圖。結果如下。我們發現，由於離散化和样本量小，即使是無害的單峰曲線也會導致相當高的直方圖。

R代碼：

  dens <-密度（等級）opar <- par（mfrow = c（2,4））for（ii in 1：8）{samp <- rnorm（length（grades ），樣本（等級，大小=長度（等級），替換= TRUE），dens $ bw）歷史（pmin（10，pmax（0，samp）），breaks = 0：10，xlab =“”，ylab =“ “，main =”“，col =” gray“）} par（opar） 

這裡有幾個可能的因素：鑑於可用的點數相對較少，集總會影響成績的分佈方式，尤其是如果它們也以整數遞增的方式。 （也就是說，模型中沒有足夠的細化方法來區分事物。）

另一個問題是樣本量相對較小。 24名學生並不是一個特別大的樣本，您的標準差是10分中的2分！另外，您應該嘗試根據半整數格（0.5到1.5、1.5到2.5等）來繪製數據。您最終會得到一個非常的分佈。

因此，基本上，我不會嘗試從這種圖或分佈中得出任何明確的結論。

我對您的數據做了一個內核密度估計圖，如下所示。您的候選人集中度較高，為4-5歐元，而表現差強人意的學生則較低。

只需在此處添加其他統計分析...您就不能確定該樣本不是來自相似班級相似學生的正態分佈總體。以下是一些用於分析及其輸出的R代碼： x = c（1.2,1.4,1.4,1.9,2.0,2.3,2.6,2.6,3.4,4.2，4.2,4.3,4.6,4.6,4.8,4.8， 4.9,5.3,6.0,6.2,6.4,7.1,7.8,7.8）; qqnorm（x）; qqline（x）

將您的成績與以下內容進行比較： by Skbkekas

您的左側成績與 QQ線不太吻合，但並不是系統地偏離。右邊的數字來自正態分佈；除了數量更多之外，它們看起來很相似。

您的成績基本上不會歪斜（歪斜（x） = .12）。它們是 platykurtic，但是您沒有足夠的數量來忽略這樣的可能性，即與正態分佈的差異是由採樣誤差引起的，這很有把握。以下是 Anscombe–Glynn峰度測試（ require（moments）; anscombe.test（x））的結果：峰度= 2.03， z = -1.23， p = 0.22。 FWIW，您還可以使用 Shapiro–Wilk檢驗（ shapiro.test（x）： W）檢驗數據來自正態分佈總體的原假設。 = .95， p = .27），但是正常性檢驗可能“基本上沒有用”（這也可能適用於峰度或偏度的專用顯著性檢驗）。

您似乎將模式或局部最大值稱為曲線。 @ StephanKolassa，@ aeismail和@JackAidley已經展示了這方面的誤導性直方圖。 @RedSirius的評論也是即時的，您已經在評論中確認了bin大小的影響，但是還沒有編輯您的問題以澄清這對您沒有幫助^{（提示；;） ;） sup>。目前尚不清楚在這裡還需要說些什麼。您沒有太多證據表明有任何不尋常的事情，更不用說為擬議的關於為不同才能的學生作弊或服務不均衡而做出的解釋提供了嚴肅的外部依據，因此似乎進一步的猜測只能抓住眾所周知的稻草。}

但是，仍然有必要背誦一些（可能沒有充分研究的）學術真理：

1. 當學生的數量遠遠超過導師時，很難使所有人都適合。
>
2. 對於努力付出幾乎為零的學生來說，您真的無能為力。
3. 如果這是努力的主要形式，作弊可能也就沒有多大作用了。
li> ol>

請記住，中心極限定理假定獨立樣本。對於學生來說，這通常是一個錯誤的假設。作弊當然是可能的，但也可能是他們成群學習（大多數人認為這很有幫助）。您數據中的峰值可能恰好對應於一起學習且具有相似優勢和劣勢的群體。

我有一種理論可以解釋這種情況下的教室異常情況，因為我有時間去思考，所以這種情況在情況上是準確的。

為簡化問題的數學運算，我省略了一些量表我數學中的一些因素，它們只不過是視覺上的混亂。

讓理想的鐘形曲線由 C（x）定義。

您的一組學生是 S ，並且對於 s∈S ，您具有一個神奇的函數 Q（s），它產生了學生作品的“質量”。

現在考慮進行測試。該測試由一系列問題組成（將此問題稱為 T ）。每個問題 p∈T 都有一個難度，由 D（p）給出。定義學生 s 正確回答問題的概率：

P _{正確 sub>（s，p）= i>}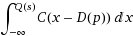

然後得出結論：問題的 Q 高於問題的 D 的學生將更有可能解決該問題，並且較低的 Q 將不太可能。

讓我們將參加考試的學生的理想分數定義為 S i sub>（s ，T）=ΣP 正確的 sub>（s，p），p∈T

如果您要為參加考試的每個學生在特定考試中取得理想成績您的教室，您將獲得理想的分佈，並且很有可能，如果您的學生實際參加了考試，您將獲得的分佈至少大致接近理想的分佈。

帶走的重要內容從目前的情況來看，對於一群參加考試的學生而言，考試中問題的難度在數學上影響您可能擁有的成績分佈。

例如，assumi ng您的學生人數大致上是彎曲的，如果您的測試問題大致具有以下難度級別，您可能會看到類似觀察結果的成績分佈：

  [2，2，5，6，6， 7，7，8，10，10+，10 +]  

大量學生會正確地解決兩個簡單的問題，但由於幾乎沒有中低難度的問題，曲線下端的一些學生將無法解決任何較難的問題。在最高端，對於學生的技能水平，有些問題可能會非常困難（這可能由於多種原因而發生），因為大多數班級都錯了（假設總分不超過10分） 。

假設您的類分佈是這樣的，

  0-2 | 3 | 14 | = 25 | === 46 | ==== 57 | ==== 58 | === 49 | = 210 | 1  

它們的理想分佈（如先前定義，經過四捨五入以減少結塊）看起來像這樣：

  0 | 1 | 2 | === 43 | === 44 | === 45 | === 46 | == 37 | = 28 | 19 | 10 |  

以一種無聲的方式類似於您實驗觀察到的觀測曲線。

此外，現實情況也不會具有如此優雅的數學解決方案（像是學生答對一個問題的概率），因此該模型應僅視為一種合理的，受過良好教育的近似值。你以為在分發時會想。

如果每個學生都能夠以獨立的概率p解決每個問題，那麼您將期望正態分佈。但這實際上不是一個很好的模型。

假設您的考試中有很多問題，任何體面的學生都有望解決。解決所有這些問題將使您獲得5年級。因此，您會在5年級獲得很多學生；在本課程中表現良好的每個人；有些人由於剛剛發生的愚蠢錯誤而略低一些，還有一些人準備不足並且沒有機會通過。

然後您會遇到一些非常困難的問題。普通學生解決不了他們。優秀的學生會解決一兩個或三個問題，直到時間耗盡。

即使有大量學生，這種測試也可以提高您的分佈。

困難的班級情景和相當標準的學生群體：

1. 冠軍-雄心勃勃且勤奮/聰明/有興趣
>這個主題上的每個小時都很痛苦，但是我 必須主題 ol>

如果測試不夠重要或過於困難，則上面的細目解釋了這一切。

冠軍並沒有設法將其最大化收集了大約6-7分的不錯分數。僅僅學生們就學到了足夠的知識以使考試減半。成績欠佳的人發現，如果不掌握主題，他們就不會在這裡閃耀。 >



水平高嗎？考試的結構是否合理，並提出了不同難度的問題？

如果是這樣，那麼我認為是這樣，您只是設法查看了您的學生是誰。您可能想找出問題是缺乏動力還是無法跳入主題。

我認為您已經將問題的難度與班級的能力範圍相提並論。這與@ gnasher729的理論類似。

顯然，所有這些都是基於數據的猜測，您必須自己決定是否有意義。但是，如果您有兩個非常簡單的問題（每個人都可以解決），這三個數據將是一致的，三個問題要難一些，仍然要困難三個，還有兩個不可能有人解決的問題。每個人都屬於三個級別之一，其中一些學生還在他們知道如何解決的問題上犯了一個或兩個錯誤。

如果某一點與一個問題不符，那是同一件事仍然可能是這樣，但問題數量不同。

因此，您嘗試分散問題的難度（正常情況下），但是a）您將許多相同難度的問題集中在一起b）你把團塊分佈得太多了，十分之四的問題根本沒有說明學生的相對能力（因為每個人都得到了其中的兩個，而沒有一個人得到了另外兩個）。我的猜測是，考試的時限不是一個很大的因素，因為人們以不同的速度工作，因此時限可能會平滑成績。

有任何簡單的方法可以測試該理論。獲得2、5和8的學生是否都得到了相同或非常相似的問題集？我的理論認為他們確實做到了。 （相當多的人犯了1或2個點的錯誤），4.8個問題（大多數沒有犯很多錯誤）和2.6個問題（大多數犯了0.5-1.5分的錯誤）。

我認為，問題的部分在於如何對圖形進行四捨五入。除了四捨五入外，我們僅舍入到最接近的整數。

這看起來更像是正態分佈，即使後端可能有點沉重。老實說，在處理類的分佈時，這樣的捨入會更有意義，因為如果沒有這種舍入，可能會出現類似於您的圖形的內容。這也解釋了為什麼許多非整數圖看起來也很正常。